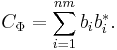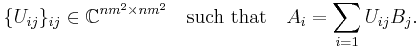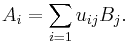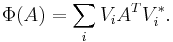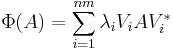Choi's theorem on completely positive maps
In mathematics, Choi's theorem on completely positive maps (after Man-Duen Choi) is a result that classifies completely positive maps between finite-dimensional (matrix) C*-algebras. An infinite-dimensional algebraic generalization of Choi's theorem is known as Belavkin's "Radon–Nikodym" theorem for completely positive maps.
Contents |
Some preliminary notions
Before stating Choi's result, we give the definition of a completely positive map and fix some notation. Cn × n will denote the C*-algebra of n × n complex matrices. We will call A ∈ Cn × n positive, or symbolically, A ≥ 0, if A is Hermitian and the spectrum of A is nonnegative. (This condition is also called positive semidefinite.)
A linear map Φ : Cn × n → Cm × m is said to be a positive map if Φ(A) ≥ 0 for all A ≥ 0. In other words, a map Φ is positive if it preserves Hermiticity and the cone of positive elements.
Any linear map Φ induces another map
in a natural way: define
and extend by linearity. In matrix notation, a general element in
can be expressed as a k × k operator matrix:
and its image under the induced map is
Writing out the individual elements in the above matrix-of-matrices amounts to the natural identification of algebras
We say that Φ is k-positive if 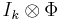 , considered as an element of Ckm×km, is a positive map, and Φ is called completely positive if Φ is k-positive for all k.
, considered as an element of Ckm×km, is a positive map, and Φ is called completely positive if Φ is k-positive for all k.
The transposition map is a standard example of a positive map that fails to be 2-positive. Let T denote this map on C 2 × 2. The following is a positive matrix in  :
:
The image of this matrix under 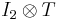 is
is
which is clearly not positive, having determinant -1.
Incidentally, a map Φ is said to be co-positive if the composition Φ 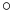 T is positive. The transposition map itself is a co-positive map.
T is positive. The transposition map itself is a co-positive map.
The above notions concerning positive maps extend naturally to maps between C*-algebras.
Choi's result
Statement of theorem
Choi's theorem reads as follows:
Let
be a positive map. The following are equivalent:
i) 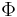 is n-positive.
is n-positive.
ii) The matrix with operator entries
is positive, where 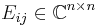 is the matrix with 1 in the
is the matrix with 1 in the 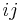 -th entry and 0s elsewhere. (The matrix
-th entry and 0s elsewhere. (The matrix 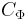 is sometimes called the Choi matrix of
is sometimes called the Choi matrix of 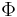 .)
.)
iii) 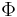 is completely positive.
is completely positive.
Proof
To show i) implies ii), we observe that if
then E=E* and E2=nE, so E=n-1EE* which is positive and CΦ=(In⊗Φ)(E) is positive by the n-positivity of Φ.
If iii) holds, then so does i) trivially.
We now turn to the argument for ii) ⇒ iii). This mainly involves chasing the different ways of looking at Cnm×nm:
Let the eigenvector decomposition of CΦ be
where the vectors 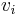 lie in Cnm . By assumption, each eigenvalue
lie in Cnm . By assumption, each eigenvalue 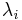 is non-negative so we can absorb the eigenvalues in the eigenvectors and redefine
is non-negative so we can absorb the eigenvalues in the eigenvectors and redefine 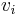 so that
so that
The vector space Cnm can be viewed as the direct sum 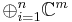 compatibly with the above identification
compatibly with the above identification 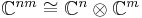 and the standard basis of Cn.
and the standard basis of Cn.
If Pk ∈ Cm × nm is projection onto the k-th copy of Cm, then Pk* ∈ Cnm×m is the inclusion of Cm as the k-th summand of the direct sum and
Now if the operators Vi ∈ Cm×n are defined on the k-th standard basis vector ek of Cn by
then
Extending by linearity gives us
for any A ∈ Cn × n. Since any map of this form is manifestly completely positive, we have the desired result.
The above is essentially Choi's original proof. Alternative proofs have also been known.
Consequences
Kraus operators
In the context of quantum information theory, the operators {Vi} are called the Kraus operators (after Karl Kraus) of Φ. Notice, given a completely positive Φ, its Kraus operators need not be unique. For example, any "square root" factorization of the Choi matrix
gives a set of Kraus operators. (Notice B need not be the unique positive square root of the Choi matrix.)
Let
where bi*'s are the row vectors of B, then
The corresponding Kraus operators can be obtained by exactly the same argument from the proof.
When the Kraus operators are obtained from the eigenvector decomposition of the Choi matrix, because the eigenvectors form an orthogonal set, the corresponding Kraus operators are also orthogonal in the Hilbert–Schmidt inner product. This is not true in general for Kraus operators obtained from square root factorizations. (Positive semidefinite matrices do not generally have a unique square-root factorizations.)
If two sets of Kraus operators {Ai}1nm and {Bi}1nm represent the same completely positive map Φ, then there exists a unitary operator matrix
This can be viewed as a special case of the result relating two minimal Stinespring representations.
Alternatively, there is an isometry scalar matrix {uij}ij ∈ Cnm × nm such that
This follows from the fact that for two square matrices M and N, M M* = N N* if and only if M = N U for some unitary U.
Completely copositive maps
It follows immediately from Choi's theorem that Φ is completely copositive if and only if it is of the form
Hermitian-preserving maps
Choi's technique can be used to obtain a similar result for a more general class of maps. Φ is said to be Hermitian-preserving if A is Hermitian implies Φ(A) is also Hermitian. One can show Φ is Hermitian-preserving if and only if it is of the form
where λi are real numbers, the eigenvalues of CΦ, and each Vi corresponds to an eigenvector of CΦ. Unlike the completely positive case, CΦ may fail to be positive. Since Hermitian matrices do not admit factorizations of the form B*B in general, the Kraus representation is no longer possible for a given Φ.
See also
References
- M. Choi, Completely Positive Linear Maps on Complex matrices, Linear Algebra and Its Applications, 285–290, 1975
- V. P. Belavkin, P. Staszewski, Radon-Nikodym Theorem for Completely Positive Maps, Reports on Mathematical Physics, v.24, No 1, 49–55, 1986.
- J. de Pillis, Linear Transformations Which Preserve Hermitian and Positive Semidefinite Operators, Pacific Journal of Mathematics, 129–137, 1967.
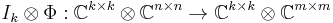
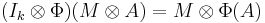
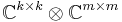
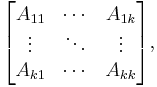
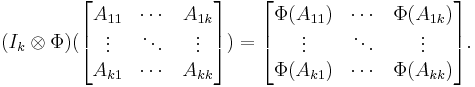
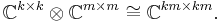
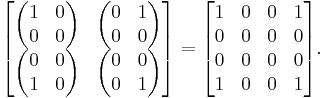
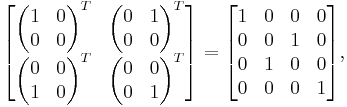
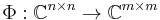
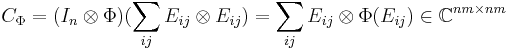
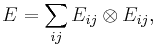
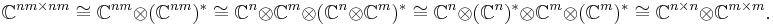
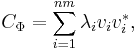
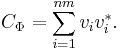
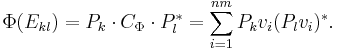
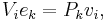
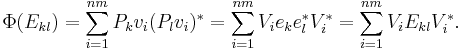
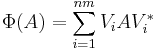
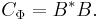
![B^* = [b_1, \ldots, b_{nm}] ,](/2012-wikipedia_en_all_nopic_01_2012/I/1d981045a381364f030aff94a249d512.png)